ローレンツ変換の式を求めます。
\(x’=\dfrac{x-vt}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(t’=\dfrac{t-\dfrac{v}{c^{2}}x}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\)
その前にニュートン力学におけるガリレイ変換について
ガリレイ変換とはニュートン力学で2つの慣性系 O-xyz(S系と呼ぶ)とO’-x’y’z’(S’系と呼ぶ)の間に成り立つ関係です。
S系とS’系の軸が平行で、S’系がS系に対してx軸方向に一定の速さvで運動しているとき、
x’=x-vt、y’=y、z’=z、t’=t と表されます。(t=0でS系とS’系の原点が一致の場合)
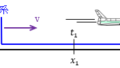
S系でx軸に平行に速さuで運動している物体PをS’系で観測した速さu’ は
u’=u-v
となります。 uを光速としたとき(u=c)、S’系で観測する光速は c’=c-u となり、光速度不変の原理は成り立ちません。
ローレンツ変換の式を求めていきます。
● 慣性系Sに対して x軸方向に一定の速さvで運動する慣性系S’があります。S系の原点をO、S’系の原点をO’とおき、OとO’がすれ違う瞬間をt=t’=0とおきます。
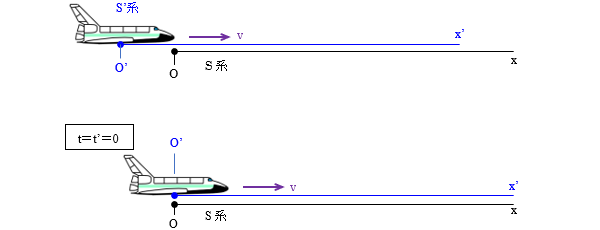
以下、座標軸のみで表示していきます。
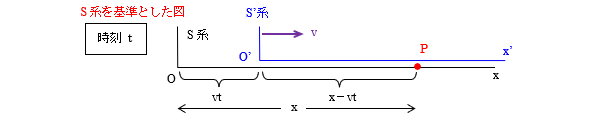
● S系を基準として、時刻t、座標xで起こった現象をP、S’系を基準としたとき、Pが起こった時刻をt’、座標をx’とおきます(t≠t’ )。(ニュートン力学では暗黙の了解としてt=t’ としていましたが、t=t’ とするとガリレイ変換と同じになり光速度不変の原理は成り立たなくなります。)
S’ 系の原点O’の位置はvtにあるので、O’とPの位置xの距離はx-vtとなっています。
● S’系を基準としてみると、原点からPまでの距離はx’で、γをある定数としてx’=γ(x-vt) の関係が成り立つものとします(x’=x-vt であればガリレイ変換と同じとなり、光速度不変の原理が成り立たなくなります)。また、S系の原点Oの位置は -vt’ にあり、OとPの距離は x’+vt’ です。 相対性原理よりx=γ(x’+vt’) も成り立つとします。

2つの図では x’=x-vt、x=x’+vt’ のように見えますが、S系で時刻tのときは同時刻の相対性からS’系での時刻は座標に依存しますので、x’ と x-vt、またはx とx’+vt’ は等しくはなりません。
● 時刻t=t’=0のとき、Oからx方向に光を発します。
ある時間が経過したときの光の位置を前述での点Pとすると、
x’=γ(x-vt) ・・・ ①
x=γ(x’+vt’) ・・・ ②
が成り立ち、さらに光速が S系、S’系それぞれを基準としてc であるので、
x = ct ・・・ ③
x’=ct’ ・・・ ④
が成り立ちます。

● ①~④ の 4式が成り立つ γ を求めます。
③ より \(t=\dfrac{c}{x}\) を ① に代入
\(x’=\gamma\left( x-\dfrac{v}{c}x\right) =\gamma\ x\left( 1-\dfrac{v}{c}\right)\) ・・・ ①’
④ より \(t’=\dfrac{c}{x’}\) を ② に代入
\(x=\gamma\left( x’+\dfrac{v}{c}x’\right) =\gamma\ x’\left( 1+\dfrac{v}{c}\right)\) ・・・ ②’
①’、②’ の両辺をかけて
\(xx’=\gamma ^{2}xx’\left( 1-\dfrac{v}{c}\right) \left( 1+\dfrac{v}{c}\right)\)
\(\gamma ^{2}=\dfrac{1}{1-\dfrac{v^{2}}{c^{2}}}\)
\(\gamma=\dfrac{1}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) をそれぞれ ①、② に代入して
\(x’=\dfrac{x-vt}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(x=\dfrac{x’+vt’}{\sqrt{1+\dfrac{v^{2}}{c^{2}}}}\)
2式より t、t’ について変形すると。
\(t’=\dfrac{t-\dfrac{v}{c^{2}}x}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(t=\dfrac{t’+\dfrac{v}{c^{2}}x’}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\)
が得られます。
(x、t)↔(x’、t’)への変換でまとめると、
ローレンツ変換
\(x’=\dfrac{x-vt}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(t’=\dfrac{t-\dfrac{v}{c^{2}}x}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\)
ローレンツ逆変換
\(x=\dfrac{x’+vt’}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(t=\dfrac{t’+\dfrac{v}{c^{2}}x’}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\)
となります。
また、\(\dfrac{v}{c}=\beta\) とおくと
ローレンツ変換
\(x’=\dfrac{x-\beta ct}{\sqrt{1-\beta ^{2}}}\) \(ct’=\dfrac{ct-\beta x}{\sqrt{1-\beta ^{2}}}\)
ローレンツ逆変換
\(x=\dfrac{x’+\beta ct’}{\sqrt{1-\beta ^{2}}}\) \(ct=\dfrac{ct’+\beta x’}{\sqrt{1-\beta ^{2}}}\)
と書くことができます。
さらに、 \(\gamma =\dfrac{1}{\sqrt{1-\beta ^{2}}}\) とおくと
ローレンツ変換
\(x’=\gamma \left( x-\beta ct\right)\) \(ct’=\gamma \left( ct-\beta x\right)\)
ローレンツ逆変換
\(x=\gamma \left( x’+\beta ct’\right)\) \(ct=\gamma \left( ct’+\beta x’\right)\)
とシンプルな形で書くこともできます。
どの形を用いるかはケースバイケースです。