同時刻の定義
2つの異なる地点A,Bで時計の時刻を正確に合わせるときはどのようにすれば良いでしょうか。AB間の距離が一定のとき Bの時計をAに合わせます。
① AB間の距離が分かっている場合(Lとおきます)
Aの時計で時刻12時のとき、光で時報を送ります。光がAからBに伝わる時間は L/c ですので、Bが光を受取ったとき、Bの時計の時刻を12時に L/c を加えれば Aに合わせることができます。
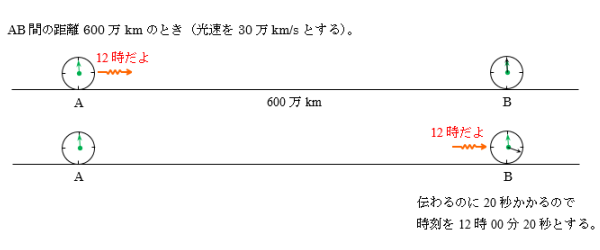
② AB間の距離が不明の場合
Bが受取った光をすぐにAに向けて反射させ、Aが受取るまでの時間TよりBまでの距離Lが分かります(L=cT/2)。あとは ① の要領で時刻を合わせることができます。
このようにすれば、Aに対して静止している全ての地点で時刻を合わせることができます。
ところがAに対してある速さで動いている人から見ると、ABの時刻は合っていないことになります!?。
同時刻の相対性
ニュートン力学ではある2つの異なる地点で同時に起こった現象は誰からみても同時刻です。ところが相対性理論ではある速さで移動する人から見ると同時ではなくなります。
これは「光速度不変の原理」より説明することができます。
簡単のためにABの2つの地点で花火を「同時に」打ち上げることで考えていきます。ABそれぞれに置かれた花火は光信号を受信すると点火するようにしておきます。
AB間の中点をOとします。中点OをAからBにある速さで移動する電車Dがあります。

ABを基準とした系で見ていきます。
電車DがOを通過する瞬間Oより光信号を発します。
光信号はABに対して光速cで伝わりABの花火は「同時」に点火します。
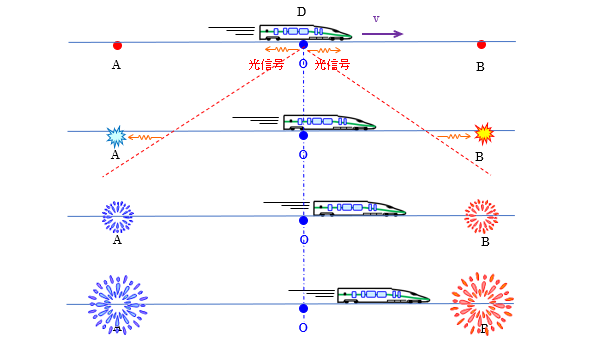
電車Dを基準とした系で見ます。
ABが左方向に移動し、光信号は電車Dに対して光速cで伝わります。
光信号はBに先に到達し花火が点火、遅れてAに到達して花火が点火します。 すなわちDを基準とした系で見るとBの事象が先に起こり、Aの事象が遅れて起こることになります。
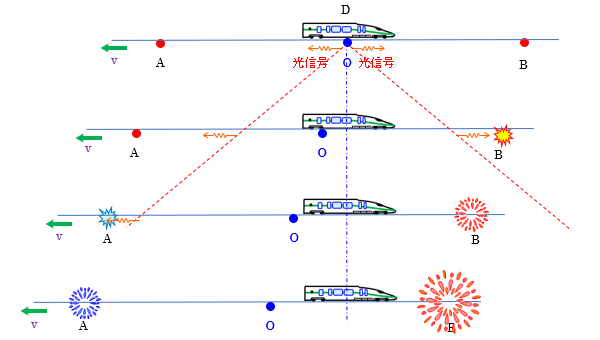
ABに置かれた花火を時計とすると、ABを基準として合わせた時刻は電車Dを基準としてみると、時刻は合っていないことになります。
どの程度の時間のずれが生じるか、AB=600万km、v=24万km/s、c=30万km/sとして求めます。
ABを基準としてt=0秒のときABで同時にある事象が起こり、このとき電車DがOを通過しているものとします。電車Dの時刻も0秒に合わせておきます。ローレンツ変換ではABがS-系、DがS’-系となります。

電車Dを基準としてみます。
事象Bが起こった時刻はAB基準で、tB=0秒、xB=300万kmですので、電車D基準では
\(t_{B}’=\dfrac{t_{B}-\dfrac{v}{c^{2}}x_{B}}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}=\dfrac{0-\dfrac{24}{30^{2}}\times 300}{\sqrt{1-0.8^{2}}}=-13.3\) 秒
となり、電車DがOに到着する13.3秒前に起こったことになります。
同様に事象Aが起こった時刻は
\(t_{A}’=\dfrac{t_{A}-\dfrac{v}{c^{2}}x_{A}}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}=\dfrac{0-\dfrac{24}{30^{2}}\times (-300)}{\sqrt{1-0.8^{2}}}=13.3\) 秒
となり、電車DがOを通過してから13.3秒後に起こったことになります。
ABの事象が起こる時間差は26.6秒です。
もし無限の速さで信号を伝える手段があれば、電車DがOを通過する前にBで将来起こることを伝えることはできるかも知れませんが、光速を超える速さはないので起こる前に伝えることは不可能となります。

