ローレンツ変換から導かれるいくつかの事柄を求めていきます。
ここでは \(\dfrac{v}{c}=\beta\) とおいたローレンツ変換の式を用います。
● 時間の遅れ:運動する系は時間が遅れる
S系を基準として、S系の時刻が t のときS’系の原点O’ の位置は x=vt となります。

S’系での時刻は
\(ct’=\dfrac{ct-\beta \cdot vt}{\sqrt{1-\beta ^{2}}}=\dfrac{ct\left( 1-\beta ^{2}\right) }{\sqrt{1-\beta ^{2}}}=ct\sqrt{1-\beta ^{2}}\)
\(t’=t\sqrt{1-\beta ^{2}}\) \(\sqrt{1-\beta ^{2}}\leqq 1\) であるので \(t’\leqq t\)
S’系はS系より時間の経過が \(\sqrt{1-\beta ^{2}}\) の割合遅れます。
例えば \(\beta =0.8\) のとき t’=0.6t となり、S系で10分経過したとき、S’系での経過時間は6分となります。
S’系を基準として、S’系の時刻が t’ のときS系の原点Oの位置はx’=-vt’ となります。

S系での時刻は
\(ct=\dfrac{ct’+\beta \cdot (-vt’)}{\sqrt{1-\beta ^{2}}}=\dfrac{ct’\left( 1-\beta ^{2}\right) }{\sqrt{1-\beta ^{2}}}=ct’\sqrt{1-\beta ^{2}}\)
\(t=t’\sqrt{1-\beta ^{2}}\) \(t\leqq t’\)
S系はS’系より時間の経過が \(\sqrt{1-\beta ^{2}}\) の割合遅れます。
S系、S’系がお互いに運動しているとき、S系を基準とすればS’系の時間が遅れ、S’系を基準とすればS系の時間が遅れます。
● 空間の短縮:運動する系は短縮する
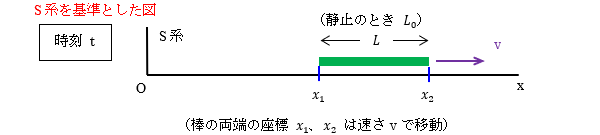
静止のときの長さが L0 の棒がS系に対して速さ v で x 軸方向に運動しています。
運動しているときの棒の長さを求めていきます。
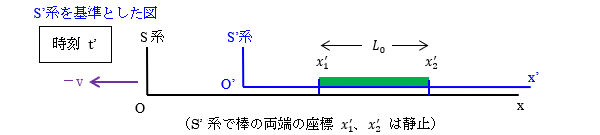
棒と同じ速さvで運動するS’系を考えます。S’系では棒は静止しており、棒の長さは L0 です。棒の両端の座標をx1‘, x2‘ とします。x1‘, x2‘ は変化しません。
\(L_{0}=x_{2}’-x_{1}’\)
S系で棒の長さを求めます。時刻 t での棒の両端の座標を x1、x2 とします。
S系で棒の長さは L=x2-x1 です。x1, x2 は速さ v で移動していきます。
ローレンツ変換より
\(x_{1}’=\dfrac{x_{1}-\beta ct}{\sqrt{1-\beta ^{2}}}\) \(x_{2}’=\dfrac{x_{2}-\beta ct}{\sqrt{1-\beta ^{2}}}\)
これより \(L_{0}=x_{2}’-x_{1}’=\dfrac{x_{2}-x_{1}}{\sqrt{1-\beta ^{2}}}=\dfrac{L}{\sqrt{1-\beta ^{2}}}\)
\(L=L_{0}\sqrt{1-\beta ^{2}}\) となり \(\sqrt{1-\beta ^{2}}\) の割合短縮します。
x1’、x2’ は棒の両端とは限らず空間の座標ですので空間自体が \(\sqrt{1-\beta ^{2}}\) の割合短縮していると考えることができます。
同様にS系で静止した長さ L0 の棒をS’系で観測したときの長さL’(=x2’-x1’)を求めます。
\(x_{1}=\dfrac{x_{1}’+\beta ct’}{\sqrt{1-\beta ^{2}}}\) \(x_{2}=\dfrac{x_{2}’+\beta ct’}{\sqrt{1-\beta ^{2}}}\)
これより \(L_{0}=x_{2}-x_{1}=\dfrac{x_{2}’-x_{1}’}{\sqrt{1-\beta ^{2}}}=\dfrac{L’}{\sqrt{1-\beta ^{2}}}\) \(L=L_{0}\sqrt{1-\beta ^{2}}\) となり \(\sqrt{1-\beta ^{2}}\) の割合短縮します。
S系、S’系がお互いに運動しているとき、S系を基準とすればS’系の空間が短縮し、S’系を基準とすればS系の空間が短縮します。短縮の割合は \(\sqrt{1-\beta ^{2}}\) です。
● 速度の合成
S系でx軸方向に一定の速さuで運動する物体を、S’系を基準としたときの物体の速さu’を求めていきます。
[ I ] S系を基準として物体が x1、x2 を通過する時刻を t1、t2とおきます。

ここで \(u=\dfrac{x_{2}-x_{1}}{t_{2}-t_{1}}\) です。 ・・・①
[II] S’系を基準として見ます。
x1、x2、t1、t2 をそれぞれローレンツ変換します。
\(x_{1}’=\dfrac{x_{1}-\beta ct_{1}}{\sqrt{1-\beta ^{2}}}\) \(x_{2}’=\dfrac{x_{2}-\beta ct_{2}}{\sqrt{1-\beta ^{2}}}\) ・・・②
\(ct_{1}’=\dfrac{ct_{1}-\beta x_{1}}{\sqrt{1-\beta ^{2}}}\) \(ct_{2}’=\dfrac{ct_{2}-\beta x_{2}}{\sqrt{1-\beta ^{2}}}\) ・・・③
S’系での物体の速さは \(u’=\dfrac{x_{2}’-x_{1}’}{t_{2}’-t_{1}’}\) です。・・・④
[III] ④ 式に ②、③ を代入します。
\(u’=\dfrac{x_{2}’-x_{1}’}{t_{2}’-t_{1}’}=\dfrac{\left( x_{2}-\beta ct_{2}\right) -\left( x_{1}-\beta ct_{1}\right) }{\left( t_{2}-\dfrac{\beta }{c}x_{2}\right) -\left( t_{1}-\dfrac{\beta }{c}x_{1}\right) }\)
\(=\dfrac{\left( x_{2}-x_{1}\right) -\beta c\left( t_{2}-t_{1}\right) }{\left( t_{2}-t_{1}\right) -\dfrac{\beta }{c}\left( x_{2}-x_{1}\right) }=\dfrac{\left( \dfrac{x_{2}-x_{1}}{t_{2}-t_{1}}\right) -\beta c}{1-\dfrac{\beta }{c}\left( \dfrac{x_{2}-x_{1}}{t_{2}-t_{1}}\right) }\)
\(\beta =\dfrac{v}{c}\) と ① 式 \(u=\dfrac{x_{2}-x_{1}}{t_{2}-t_{1}}\) を代入して、
\(u’=\dfrac{u-v}{1-\dfrac{v}{c^{2}}u}\) が得られます。
ここで u=c(光速)とおくと
\(u’=\dfrac{c-v}{1-\dfrac{v}{c^{2}}c}=c\) となり、S系でもS’系でも光速度は不変です。
