— ルンゲ・クッタ法による近似計算 —
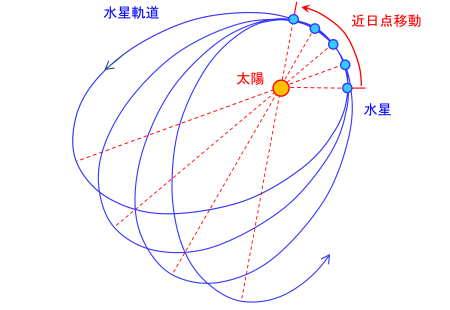
水星の近日点移動は一世紀に約575秒と観測されています。
532秒が金星、木星など他の惑星による影響で、残り43秒は一般相対性理論によって説明することができます。ニュートン力学ではそれぞれの惑星による水星の近日点の移動は以下のようになっています。(Wikipedia 近点移動)
金星 276.38秒
地球 91.41秒
火星 2.48秒
木星 153.98秒
土星 7.31秒
天王星 0.14
海王星 0.04秒ここでは万有引力のみを考慮して各惑星の水星の近日点移動をルンゲ・クッタ法で求めてみました。
計算の方法としては、太陽-水星-惑星の3体問題として扱っています。
例えば金星の影響による近日点移動を求める場合は「太陽-水星-金星の3体問題」、木星の影響は「太陽-水星-木星の3体問題」などのように求めていきます。
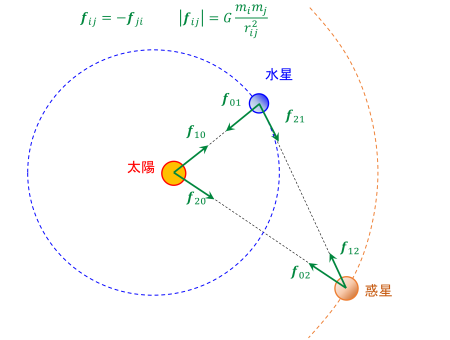
角度の秒と時間の秒があるので紛らわしいので、必要に応じて「時間」か「角度」を付け加えておきます。
簡単のため、運動は同一平面内とし、ある時刻でそれぞれの天体が他の2個の天体より受ける万有引力より加速度を求め、Δt=1秒(時間)で速度と位置をルンゲ・クッタ法で求めていきました。
Δt=1秒(時間)は、水星の近日点で1秒間(時間)の公転による回転角が0.26秒(角度)で土星や火星による近日点の変化まで求めるためにはこれくらいの精度が必要であり、他に計算時間も考慮して決めました。100年間の変化を求める計算時間は手持ちのパソコンでは40分弱です。
プログラムは C++ でメインの部分は 300行ぐらいです。
具体的な手順は以下のとおりです。
・初期条件として、太陽を中心におき、水星、惑星の近日点を同一方向にそろえる。(惑星の近日点距離、最大速度は NASA の Planetary Fact Sheets の値を使用)
・太陽、水星、惑星の重心と重心速度を求める。
・重心を原点におき、重心に対する運動として求める。
・Δt=1秒として各惑星に働く万有引力より加速度、速度、位置を求めていく。
・水星の近日点の位置を1公転毎にファイルに記録し、水星の415公転(100年)まで求める。
・gnuplot で結果を表示
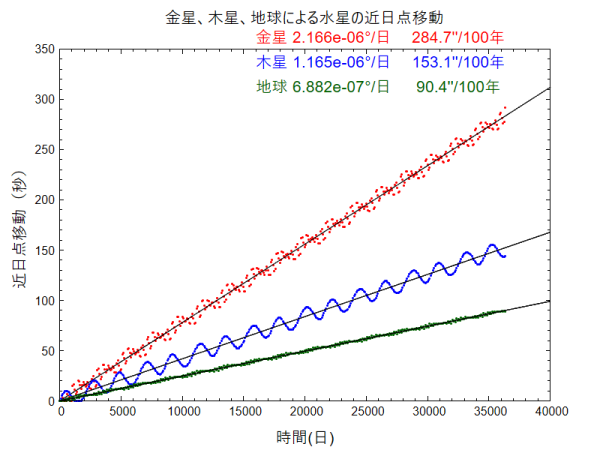
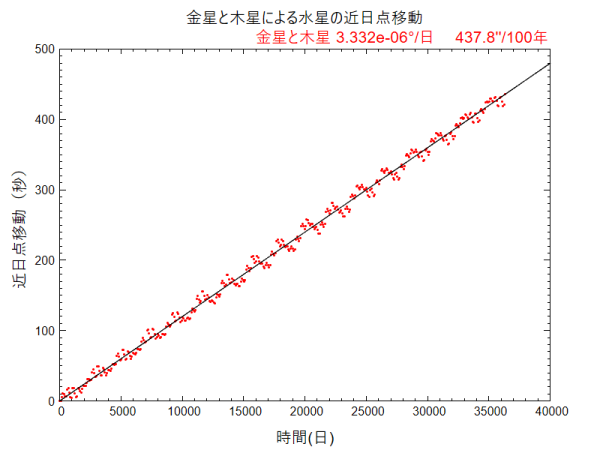
下の図が計算結果です。金星、木星、地球による水星の近日点の変化を横軸に時間(日)、縦軸に近日点の変化(角度の秒)をとって表しています。
おおむね直線上に変化していますが、直線の周りに波打つように変化しています。
おそらく、水星と各惑星の位置関係によるものと思います。100年間の変化は全体を直線フィットし、傾きに36,500日を掛けて求めています。ルンゲ・クッタ法による計算値とWikipedia の値( )内と比べると、
金星 285秒(276秒)
木星 153秒(154秒)
地球 90.4秒(91.4秒)結構いい値が出ていると思います。
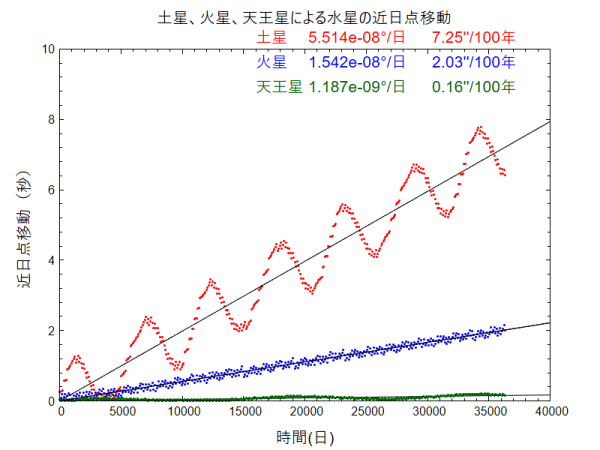
同じく土星、火星、天王星による水星の近日点の変化です。
ルンゲ・クッタ法による計算値とWikipedia の値( )内と比べると、
土星 7.25秒(7.31秒)
火星 2.03秒(2.48秒)
天王星 0.16秒(0.14秒)となっています。天王星は Δt=0.2秒(時間)で求めています。計算時間は3時間弱です。
火星、天王星の影響も思ったよりいい値で求められることができました。海王星の影響もΔtをさらに小さくすれば求められるかもしれませんが時間がかかるのでパスします。
念のため、太陽-水星-金星-木星の 4体問題で水星の近日点移動を求めてみました。5体以上でも計算はできるのですが、処理時間が長くなるので 4体までにしておきます。金星、木星それぞれで求めた値の合計(284.7+153.1=437.8”/100年)に等しくなっています。
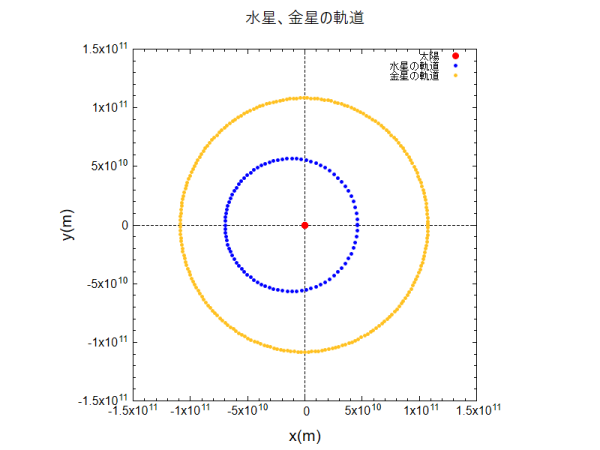
下の図は金星による水星の近日点移動の際に求めた太陽、水星、金星の軌道をそれぞれ最初の1周目について1日毎にプロットした図です。初期値は水星と金星の近日点とその点での速度のみで、あとはそれぞれに働く万有引力から求めています。特に水星では近日点で点の間隔が広く、遠日点で点の間隔が狭くなっていることから面積速度一定の法則が成り立っているように見えます。このことに関しては別のカテゴリーで調べてみることにします。
太陽、水星、金星の重心に対する「太陽の中心」の動きを拡大したのが下の図です。
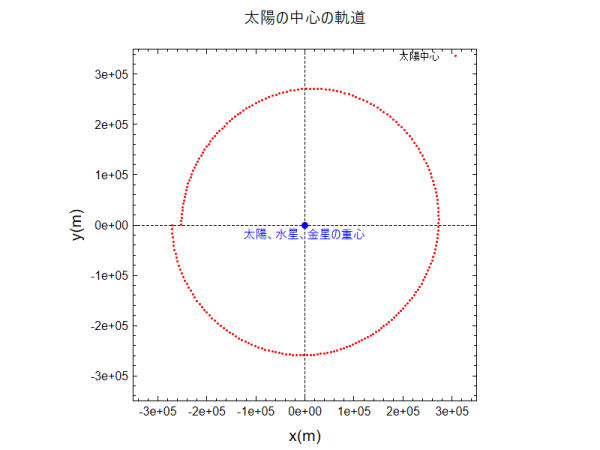
太陽の半径が \(6.96\times 10^{8}m\) ですので重心は太陽の内部です。 2つの惑星の引力だけでも太陽の動きがルンゲ・クッタ法で求められていることが分かります。
以上の計算で、各惑星がお互いに重力で影響を及ぼしながら、わずかなずれとはいえ複雑に軌道が変化していることが実感できました。

