振幅の小さい微小振動では単振動として扱うことができ等時性が(近似的に)成り立ちます。振幅が大きくなるにつれて周期は長くなり等時性は成り立たなくなりなります。
振幅の大きいときの振子の運動は求めたことがないので、ルンゲ・クッタ法で周期を求めて解析的な計算で求めた値と比較してみました。
まず、解析的な方法での周期の計算です。
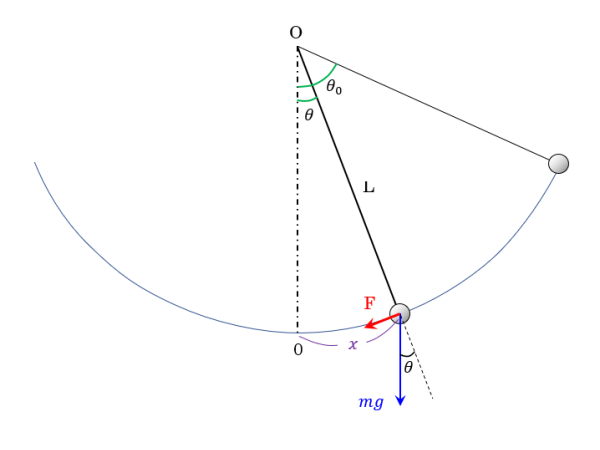
長さ L、おもりの質量 m の振子の運動を求める運動方程式は次のようになります。(おもりの大きさ、空気抵抗は無視)
\(m\dfrac{d^{2}x}{dt^{2}}=-mg\sin \left( \dfrac{x}{L}\right)\)
\(x=L\theta\)、両辺を mL で割ると
\(\dfrac{d^{2}\theta }{dt^{2}}=-\dfrac{g}{L} \sin \theta\)
のように θ に関する2階微分方程式となります。
θ は時間で2回微分すると元の形 θ に戻ったものが sin の中にあるという関数で、解析的に解を求めることはできませんが、振幅 \(\theta _{0}\) の周期 T は次の式のように級数展開した形で求めることはできます。
\(T_{0}=2 \pi \sqrt{\dfrac{L}{g}}\) とすると、
\(T=T_{0} \sum ^{\infty }_{n=0}\left\{ \dfrac{\left( 2n-1\right) !!}{\left( 2n\right) !!}\right\} ^{2}\left( \sin \dfrac{\theta _{0}}{2}\right) ^{2n}\)
!! は二重階乗で
\(k!!=k\left( k-2\right) \left( k-4\right) \cdot \cdot \cdot 4\cdot 2\) (k:偶数)
\(k!!=k\left( k-2\right) \left( k-4\right) \cdot \cdot \cdot 3\cdot 1\) (k:奇数)
\(0!!=1\) (定義)
です。
振子の長さ L=1m の周期を上の式で求めた値です。まず、微小振動での周期を求めると(\(g=9.80665 m/s^{2}\))
\(T_{0}=2 \pi \sqrt{\dfrac{L}{g}}=2.00641s\)
となります。振幅を大きくしていくと周期がこの値より少しずつ長くなっていきます。
振幅 θ0 周期 T(秒)
1° 2.00645
3° 2.00675
5° 2.00736
10° 2.01024
30° 2.04134
90° 2.36825
120° 2.75456
150° 3.53570 振幅が5°以内であれば周期は T0 と比べて 0.05% 以内の違いですが、これを超えると違いが大きくなっています。
今度はルンゲ・クッタ法で周期を求めてみます。振子の長さ1m、おもりの質量1kgで振幅60°の場合について求めたコードです。Δt=0.0001 秒で求めています。
#include <stdio.h>
#include <math.h>
#include <memory.h>
#define PI 3.14159265358979323846
#define R2D 57.29577951
double g,m;
double L;
//--- functions ---------------------------------
double ar(double r);
double fact2(int n); // 2重階乗
//-----------------------------------------------
int main()
{
long i,n;
//---
double T0,T1; // sec 周期(計算値)
double the_max; // 振幅 [rad]
//---
long nround; // 往復回数
double the0,r0,vr0; // 初期条件, the0[deg]
double r,vr,theta,thedeg; // r=L*theta 円周方向の位置、the
double t_pre,r_pre,vr_pre; // 1step 前の時間、位置、速度
double sint2; // sin(the_max/2.0)*sin(the_max/2.0)
double t,x,y;
double dr,dvr,dt;
double dr1,dvr1;
double dr2,dvr2;
double dr3,dvr3;
double dr4,dvr4;
//---------------
double dr0_pre,dr0; // 1step 前後での r-r0
double tround[1000]; // nround(=0,1,2,…) r0 を通過する時間(1000周期まで)
double dtround[1000]; // tround[n]-tround[n-1] 1往復の時間
double avT10; // 10周期の平均
//---------------
double E,Ke,Ue; // [J] 力学的エネルギー、運動エネルギー、位置エネルギー
double ss;
double omega; // 計算値
double fsmpl,dfsmpl,dthe; // 単振動との比較
//---------------
g = 9.80665; // m/s2 標準重力加速度
m = 1.0; // kg(おもりの質量)
L = 1.0; // m (振子の長さ)
//=== 初期値 =================================
//--- 振幅 ---
the0 = 60.0; // 度
//------------
t = 0.0;
dt = 0.0001; // sec
r0 = L*the0*PI/180.0;
vr0 = 0.0; // m/s
//============================================
//=== 周期の計算(解析的)====================
//--- 微小角度での周期 ---
T0 = 2.0*PI*sqrt(L/g); // 単振動
the_max = r0/L;
//--- 解析的な式より求めた周期 ---
sint2 = sin(the_max/2.0)*sin(the_max/2.0);
ss = 1.0;
//--- 2重階乗で n<150 まで求める。---
for(n=1; n<150; n++){
ss = ss+pow(fact2(2*n-1)/fact2(2*n),2.0)*pow(sint2,(double)n);
}
T1 = T0*ss;
omega = 2*PI/T1;
//============================================
//=== ルンゲ・クッタ法 =======================
//-----------------------------------
memset(&tround,0.0,sizeof(tround));
memset(&dtround,0.0,sizeof(dtround));
//-----------------------------------
r = r0;
vr = vr0;
nround = 0;
for(i=0; i<400000; i++){
if(i%500==0){
x = L*sin(theta);
y = L-L*cos(theta);
if(t<T1*0.5) printf("t=%8.4lf x=%9.5lf y=%9.5lf\n",t,x,y); // x,y(最初の半周期)
}
if(i%200==0){
fsmpl = r0*cos(omega*t);
dfsmpl = r-fsmpl;
dthe = dfsmpl/L*R2D; // 周期T0の単振動としたときの角度差
x = L*sin(theta);
y = L-L*cos(theta);
Ke = 1.0/2.0*m*vr*vr;
Ue = m*g*y;
E = Ke+Ue;
thedeg = r/L*R2D; // 振れ角(度)
//--- 運動、位置、力学的エネルギー(必要であれば出力)---
/*printf("t=%8.4lf θ=%11.6lf dθ=%9.6lf Ke=%9.6lf Ue=%9.6lf E=%9.6lf\n",\
t,thedeg,dthe,Ke,Ue,E);*/
}
//--- 1step 前の値 ---
t_pre = t;
r_pre = r;
vr_pre = vr;
//--------------------------------------------------
dr1 = vr*dt;
dvr1 = ar(r)*dt;
dr2 = (vr+dvr1/2.0)*dt;
dvr2 = ar(r+dr1/2.0)*dt;
dr3 = (vr+dvr2/2.0)*dt;
dvr3 = ar(r+dr2/2.0)*dt;
dr4 = (vr+dvr3)*dt;
dvr4 = ar(r+dr3)*dt;
//--------------------------------------------------
dr = (dr1+2.0*dr2+2.0*dr3+dr4)/6.0;
dvr = (dvr1+2.0*dvr2+2.0*dvr3+dvr4)/6.0;
//--------------------------------------------------
r = r+dr;
vr = vr+dvr;
t = t+dt;
//--------------------------------------------------
theta = r/L;
//--- r>0 での折り返し点 ---
if(vr_pre>=0.0 && vr<0.0){
dr0_pre = fabs(r_pre-r0);
dr0 = fabs(r-r0);
//--- dr0_pre=r_pre-dr と dr0=r-r0 で 小さい方 ---
tround[nround]=t_pre+dr0_pre/(dr0_pre+dr0)*dt;
nround++;
}
/*******************/
if(nround>10) break;
/*******************/
}
//------------------------------------------------------
printf("\n θ0 =%5.1lf(°)\n",the0);
printf(" T0 =%9.5lf sec (=2πsqrt(L/g))\n",T0);
printf(" T1 =%9.5lf sec (解析的に式で求めた周期)\n\n",T1);
printf(" ルンゲ・クッタ法で求めた周期(dt=%9.5lf秒)\n",dt);
for(nround=1; nround<1000; nround++){
if(tround[nround]==0.0) continue;
dtround[nround-1] = tround[nround]-tround[nround-1];
printf(" 往復数 = %4d t =%9.5lf sec\n",nround,dtround[nround-1]);
}
avT10 = tround[10]/10.0;
printf("\n 最初の10往復平均 t =%9.5lf sec\n",avT10);
return 0;
}
double ar(double r)
{
double aa;
aa = -g*sin(r/L);
return aa;
}
double fact2(int n)
{
int i;
double factorial2;
factorial2 = 1.0;
if(n<=1){
factorial2 = 1.0;
} else {
for(i=n; i>=1; i=i-2){ factorial2 = factorial2*(double)i; }
}
return factorial2;
}
結果です。
θ0 = 60.0(°)
T0 = 2.00641 sec (=2πsqrt(L/g))
T1 = 2.15324 sec (解析的に式で求めた周期)
ルンゲ・クッタ法で求めた周期(dt= 0.00010秒)
往復数 = 1 t = 2.15324 sec
往復数 = 2 t = 2.15326 sec
往復数 = 3 t = 2.15322 sec
往復数 = 4 t = 2.15327 sec
往復数 = 5 t = 2.15322 sec
往復数 = 6 t = 2.15326 sec
往復数 = 7 t = 2.15324 sec
往復数 = 8 t = 2.15323 sec
往復数 = 9 t = 2.15327 sec
往復数 = 10 t = 2.15321 sec
最初の10往復平均 t = 2.15324 sec
1往復毎の周期は多少ばらつきがありますが、10往復の周期の平均値は解析的に求めた値と一致しています。
これをいくつかの振幅について求め、1/50 秒毎に振子の振れの角度を図にプロットして見ました。
振幅が小さいときの結果です。周期は同じに見えます。
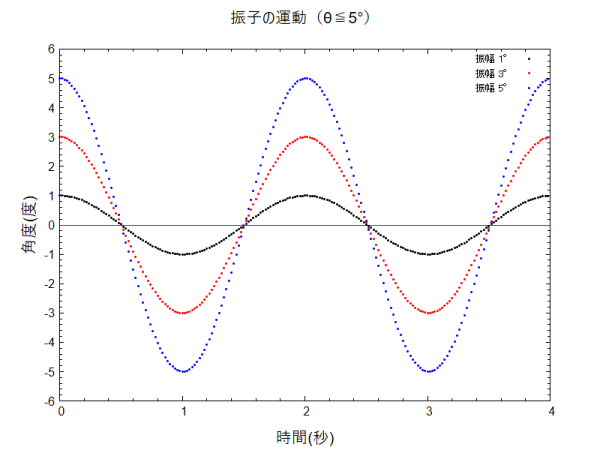
振幅の大きい場合です。振幅が大きいほど周期が長くなっていることが分かります。
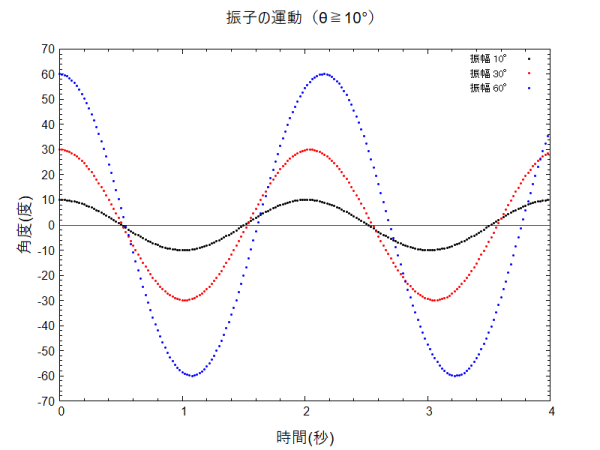
確かに振幅が小さいときは等時性が(近似的に)成り立ち、振幅が大きくなると成り立たないことが示されています。
最後にルンゲ・クッタ法で求めた周期(10往復の平均)と解析的な計算値と比較した結果をまとめてみました。振幅150°までよく一致しています。
周期T(秒)
振幅 θ0 解析的な値 ルンゲ・クッタ10往復平均
1° 2.00645 2.00645
3° 2.00675 2.00675
5° 2.00736 2.00736
10° 2.01024 2.01024
30° 2.04134 2.04134
90° 2.36825 2.36825
120° 2.75456 2.75456
150° 3.53570 3.53570
ここで思ったことが、振子の運動を求めるのは意外と難しいということです。それでもルンゲ・クッタ法ではかなり正確に求めることができるようです。ただし、振幅を160°以上にすると解析的な値とルンゲ・クッタ法で求めた値に差がでてきます。どちらかの計算に原因があるのか双方に原因があるのかは今後の課題ですが、今回はここまでにしておきます。

