相対性理論によれば、運動する系には時間の遅れが生じます。
系の速さを v、光速をcとおけば、運動する系の時間の遅れは
\(t’=\sqrt{1-\left( \dfrac{v}{c}\right) ^{2}}t\) (t は v=0 での経過時間)
となります。
相対性原理により慣性系は同等ですので、2つの慣性系S, S’ が相対速度vで運動しているとき、S-系を基準にすればS’-系の時間が遅れ、S’-系を基準にすればS-系の時間が遅れることになります。
このようなことが果たして成り立つのでしょうか?「おかしい!矛盾している!相対性理論は間違っている。」という議論が過去になされ、その名残でパラドックスと呼ばれています。
ローレンツ変換
慣性系Sに対して、一定の速さvで運動する慣性系S’があるとき、Sの原点をO、S’の原点をO’とおき、OとO’がすれ違う瞬間を t=t’=0 とします。
Sを基準として、時刻t、座標xで起こった現象Pを、
S’を基準として、Pが起こった時刻をt’、座標をx’とおくと、
\(x’=\dfrac{x-vt}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(t’=\dfrac{t-\dfrac{v}{c^{2}}x}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\)
の関係があることをローレンツ変換と呼びます。
ローレンツ逆変換
\(x=\dfrac{x’+vt’}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(t=\dfrac{t’+\dfrac{v}{c^{2}}x’}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\)
時計のパラドックス
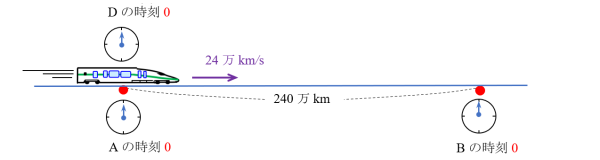
240万km離れた2つの駅A、Bがあります。電車Dが速さ秒速24万kmでAからBへ移動しています。A、B、Dには時計があり、A、Bの時刻は合わせてあります。

DがA駅を通過のときAの時刻が0を示していたので、Dの乗客はそれに合わせてDの時刻を0に合わせます。
A、Bを基準として見ていきます。
① DがAを通過のとき、Aから見ても、Dから見ても共にA、Dの時刻は0を示しています。(A、Dの距離は0であるので双方で見たAとDの時計の読み取りは同じになります。)
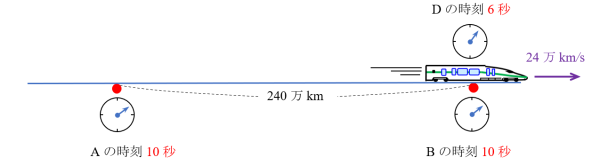
② DがBを通過のとき、AからBの移動時間が10秒ですので、Bの時刻は10秒です。Dの時間が遅れるので、
\(t_{D}=\sqrt{1-\left( \dfrac{24}{30}\right) ^{2}}\times 10=6\) 秒
より、Dの時刻は6秒です。Bから見ても、Dから見てもBの時刻は10秒、Dの時刻は6秒です。
電車Dの乗客からみると以下のようになります。
A、Bが反対方向に秒速24万kmで移動していきます。
③ DがAを通過するとき、①より D、Aの時刻はDから見ても、Aから見ても0を示しています。

④ DがBを通過するとき、②より D、Bの時刻はDから見ても、Bから見てもDの時刻は6秒、Bの時刻は10秒です。
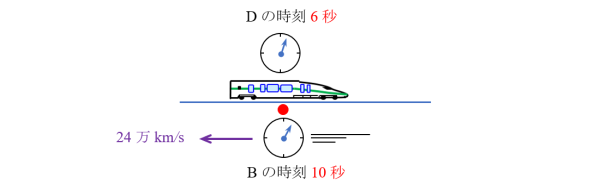
あれ? A、Bが動いているのでBの時刻はDより遅れているはずなのに? 矛盾している?
確かにDがBを通過のとき時計の針はBは10秒、Dは6秒を示していますが、矛盾はありません。これは同時刻の相対性より「Dを基準にとる」とDがAを通過しているとき、Dの時刻は0ですが、Bの時刻は0ではないことで説明できます。
ABを基準とした系をS-系、電車Dを基準とした系をS’-系とすると、DがAを通過しているときS’-系の時刻はt’=0です。
以下、Dを基準とした系(S’-系)で見た場合です。
S-系でxB=240万kmの位置で時刻tBで起こった事象がS’-系でt’=0となることから、
ローレンツ変換の式 \(t’=\dfrac{t_{B}-\dfrac{v}{c^{2}}x_{B}}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\)
に t’=0、v/c=0.8、xB=240万kmを代入すると
\(t_{B}-0.8\times \dfrac{240}{30}=0\) より tB=6.4 秒となります。
DがAを通過しているとき、Dの時刻は0ですが、Bの時刻は6.4秒です。DはBを通過のとき、Dの時計は6秒、Bの時計は10秒を示していますが、ABを移動する間のBの経過時間は 10-6.4=3.6秒 です。 3.6÷6=0.6 でBの経過時間はDより0.6 の割合で遅れています。
また、このときDからBまでの距離は
\(x’=\dfrac{x_{B}-vt_{B}}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}=\dfrac{240-24\times 6.4}{\sqrt{1-0.8^{2}}}=144 万km\)
となり、 144÷240=0.6 でS-系を基準とした距離の0.6倍に短縮しています。秒速24万km で通過する時間は6秒です。
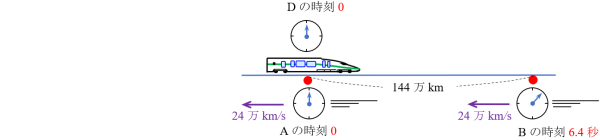
電車DからB駅の時刻は見えませんので、Dの前方144万km(Dを基準としています)をDと同じ速度で移動している電車Eを考えます。Eは丁度Bを通過しています。Eから見るとEの時刻はDと同じく0でBの時刻は6.4秒です。このことからDがAを通過のときBの時刻が6.4秒であることが確認できます。
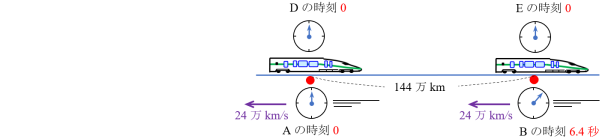
同様にDがBを通過しているとき、Dの時刻は6秒です。このとき、S-系でxA=0の位置で、ある時刻tAで起こった事象がS’-系でt’=6秒となることから、
ローレンツ変換の式に数値を代入して \( 6=\dfrac{t_{A}-0.8\times \dfrac{0}{30}}{\sqrt{1-0.8^{2}}}\)
よりAの時刻は tA=3.6秒です。
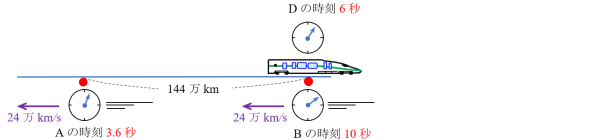
DがABを移動する時間6秒の間に、Aの時間の経過は 3.6秒です。 Aの時間の経過はDよりやはり0.6の割合で遅れています。
このようにABとDがお互いに相対運動している限り、ABを基準とすればDの時間が遅れ、Dを基準とすればABの時間が遅れることに矛盾はありません。

