単振動で空気抵抗を考慮した場合の運動を求めます。
速さに比例するとしたときの抵抗力を f’=-γ’v とおいたときの運動方程式は
\(\dfrac{d^{2}x}{dt^{2}}=-\omega ^{2}x-\dfrac{\gamma’}{m}v\)
バネの場合は \(\omega ^{2}=\dfrac{k}{m}\)、単振子の場合は \(\omega ^{2}=\dfrac{g}{L}\) です。
\(v=\dfrac{dx}{dt}\)、\(\dfrac{\gamma’}{m}=2\gamma\) とおくと \(\dfrac{d^{2}x}{dt^{2}}+2\gamma \dfrac{dx}{dt}+\omega ^{2}x=0\)
の2階線形微分方程式となります。
\(\omega ^{2} >\gamma ^{2}\) のときの一般解は \(x=Ce^{-\gamma t}\sin \left( \omega’t+\phi \right)\) (\(\omega’=\sqrt{\omega^{2}-\gamma^{2}}\))
です。
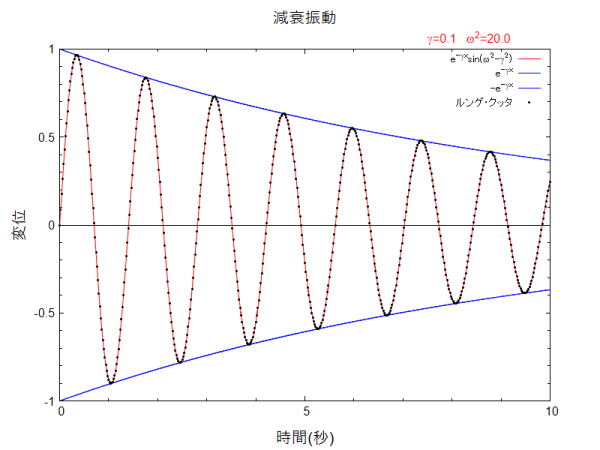
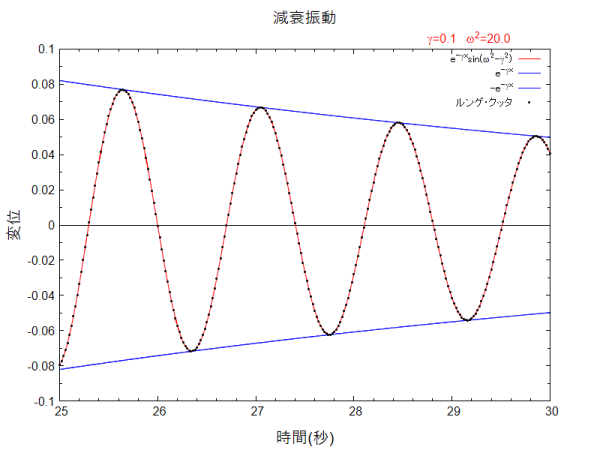
ここでは γ=0.1、\(\omega ^{2}=20\) の場合の解をルンゲ・クッタ法で求め解析解と比較します。
下が結果をグラフで表したものです。黒点がルンゲ・クッタ法で求めた値で、赤線が解析解です。解析解とよく一致しています。
作成したプログラムのコードです。結果を dvibration.xy のファイルに出力します。
dvibration.xy を読取って gnuplot で描き出すコードは下に記載してあります。
#include <stdio.h>
#include <math.h>
double dvdt(double x,double v,double gamma,double omega);
double xft(double gamma,double omega,double t);
void main()
{
int i,n;
double gamma,omega;
double t_max;
double t,v,x,xi,vi;
double dt,dv,dx;
double kx1,kx2,kx3,kx4;
double kv1,kv2,kv3,kv4;
//----------------------------
double xfunc; // 解析解
double xdeff; // Runge_Kutta - xfunc
//----------------------------
FILE *fout1;
fout1 = fopen("dvibration.xy","w");
//--- 初期値 ---
t = 0.; // [s]
dt = 0.02; // [s]
t_max = 20.0; // [s]
//--------------
gamma = 0.1;
omega = sqrt(20.0);
//--------------
x = 0.0;
v = sqrt(20.0);
n = 2000;
for(i=0; i<n; i++){
fprintf(fout1,"%8.3f %11.6f\n",t,x);
xi = x;
vi = v;
kx1 = v;
kv1 = dvdt(xi,vi,gamma,omega);
xi = x+0.5*dt*kx1;
vi = v+0.5*dt*kv1;
kx2 = vi;
kv2 = dvdt(xi,vi,gamma,omega);
xi = x+0.5*dt*kx2;
vi = v+0.5*dt*kv2;
kx3 = vi;
kv3 = dvdt(xi,vi,gamma,omega);
xi = x+dt*kx3;
vi = v+dt*kv3;
kx4 = vi;
kv4 = dvdt(xi,vi,gamma,omega);
x = x+dt*(kx1+2.0*kx2+2.0*kx3+kx4)/6.0;
v = v+dt*(kv1+2.0*kv2+2.0*kv3+kv4)/6.0;
t = t+dt;
//--- 解析解からの値 ---
xfunc = xft(gamma,omega,t);
xdeff = x-xfunc;
//----------------------------
printf("i=%3d t=%8.3f x=%11.6f v=%9.6f\n",i,t,x,v);
printf(" xdeff=%11.6f\n",xdeff);
}
//--------------------------
}
double dvdt(double x,double v,double gamma,double omega)
{
return -omega*omega*x-2.0*gamma*v;;
}
double xft(double gamma,double omega,double t)
{
return exp(-gamma*t)*sin(sqrt(omega*omega-gamma*gamma)*t);
}
gnuplot のコード
reset
set samples 10000
set rmargin 10 # 右側余白
set lmargin 12 # 左側余白
set tmargin 5 # 上側余白
set bmargin 5 # 下側余白
set xzeroaxis lt 1 lc rgb "black"
set title "減衰振動" font "Arial,16" offset 0,2
set xzeroaxis lt 1 lc "black"
set tics font "Arial,12"
set xtics 1 # x軸数値のきざみ幅
set mxtics 5 # xtics を 5等分
set ytics 0.02 # y軸数値のきざみ幅
set mytics 2 # ytics を 2等分
set xtics scale 2,1 # 大目盛、小目盛の長さを2、1
set ytics scale 2,1 # 大目盛、小目盛の長さを2、1
set xlabel "時間(秒)" font "Arial,16" offset 0,-1
set ylabel "変位"font "Arial,16" offset -2,0
set key spacing 1.5
set xrange [25:30]
set yrange [-0.1:0.1]
gamma = 0.1
omega = sqrt(20)
set label 1 sprintf("{/=12 {/Symbol g}=%3.1f {/Symbol w}^2=%4.1f}",gamma,omega*omega)\
at graph 0.75,1.03 textcolor "red" font "Arial,12"
exp_gx(x) = exp(-gamma*x)
plot exp(-gamma*x)*sin(sqrt(omega*omega-gamma*gamma)*x)\
title "e^{-{/Symbol g}x}sin({/Symbol w}^2-{/Symbol g}^2)" lc rgb "red",\
exp_gx(x) title "e^{-{/Symbol g}x}" lc rgb "blue",\
-exp_gx(x) title "-e^{-{/Symbol g}x}" lc rgb "blue",\
"dvibration.xy" title "ルンゲ・クッタ" with po ps 0.1 pt 7 lc rgb "black"

