不確定性原理とは、原子や素粒子の微視的世界で、ひとつの粒子について、位置と運動量を同時に正確に決めることが不可能であるという原理です。時間とエネルギーについても不確定性関係があります。
1927年にハイゼンベルクが導いた原理です。
1個の電子で考えてみます。
ニュートン力学の考え方
電子が電場も磁場もない空間のある位置(原点にとる)に「静止」しています。力は全く働いていません。電子は時間が経過しても原点に静止したままです。すなわち、未来の電子の位置は原点で速さは 0 です。電子の未来の位置は決まっており、「電子は見なくてもその位置にある」という考え方が根底にあります。
また、左から電子が1個飛んできて右に移動しているとき「電子の通過した道筋は見ていなくても決まっている」というのがニュートン力学の考え方です。
ところがこのことは自明でしょうか?
量子力学の考え方
量子力学では「電子の位置と運動量」は観測して初めて確定されるという考え方です。また、電子の位置と運動量は同時に正確に決めることはできません。電子の通過点は随時観測して初めて確定されますが、観測する毎に電子の運動に影響を与え、観測しないときに通過した道筋は考えることはできません。
電子の位置を観測するためにはどのようにすればよいでしょうか。真っ暗な箱に電子が1個ある場合を想定します。一番手っ取り早いのが光を当てることです。動きを調べるためにもう一度光を当てます。ニュートン力学の考え方では電子が静止していれば同じ位置で観測されるはずです。
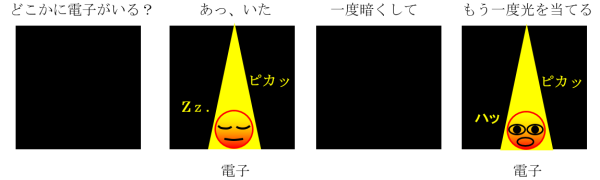
ところが、光は粒子の性質を持っているので電子に衝突すると電子をはね飛ばしてしまいます。また、波の性質も持っているので、位置の精度は波長で決まります。
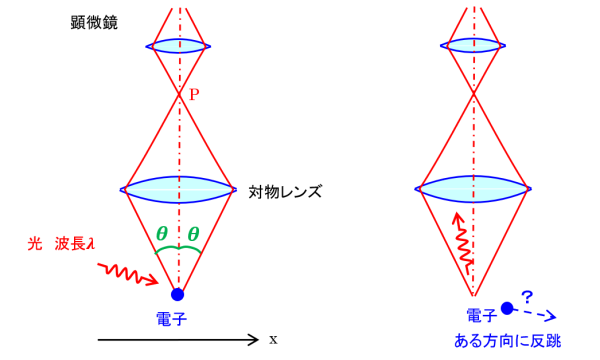
電子の位置を測定するために波長 λ の光を当て顕微鏡で観測します。
光は運動量 \(p=\dfrac{h}{\lambda }\) を持つので、以下「光子」とします。
電子に当たり反跳した光が対物レンズに入射すると電子の位置が分かります。ところが、顕微鏡の分解能は物理光学より \(\Delta x=0.6 \dfrac{\lambda }{\sin \theta }\) ですので、電子の位置に \(\Delta x\) の不確定さが生じます。
また、光子は運動量 \(p=\dfrac{h}{\lambda }\) を持つので、電子に衝突すると電子は反跳を受けます。電子に与えた運動量は光子の運動量変化から測定可能ですが、対物レンズに入射した光はすべて P(下図)の一点に集まるので、対物レンズのどの位置を通過したかは分かりません。このため運動量に
\(\Delta p_{x}=2\cdot \dfrac{h}{\lambda }\sin \theta\)
の不確定さが生じます。反跳を小さくするために波長の長い光を当てると位置が不確定となり、位置を正確に測定するために波長の短い光を当てると電子の運動量の不確定さが大きくなります。
\(\Delta x\) と \(\Delta p_{x}\) の積をとると \(\Delta x\cdot \Delta p_{x}\sim h\) となります。
実際の不確定さはこれより大きいので \(\Delta x\cdot \Delta p_{x}\geq h\) とします。また詳しい理論によると
\(\Delta x\cdot \Delta p_{x}\geq \dfrac{\hbar }{2}\) \(( \hbar = \dfrac{h}{2\pi })\)
です。
実際どれくらいの不確定さが生じるのか計算してみました。式は
\(\Delta x\cdot \Delta p_{x}\geq \dfrac{\hbar }{2}\)
を使用します。
● 電子に緑色の光を当てた場合での不確定さを求めてみます。波長は1/2000mm程度ですので、位置測定の誤差を Δx=1/2000mm(=0.5×10-6m)とすると、運動量の不確定さは以下のようになります。
\(\Delta p_{x}\geq \dfrac{\hbar }{2\Delta x}=\dfrac{1.05\times 10^{-34}}{2\times 0.5\times 10^{-6}}=1.05\times 10^{-28} kg\cdot m/s\)
\(\Delta p_{x}=m\Delta v_{x}\) 、電子の質量 \(m=9.11\times 10^{-31} kg\) より速度に関して
\(\Delta v_{x}=\dfrac{1.05\times 10^{-28}}{9.11\times 10^{-31}}\sim 115m/s\)
の不確定さを生じます。このことは一度電子の位置を 1/2000mm の精度で測定すると、1秒後の電子の位置は大雑把に±100m程度で不確定となります。もう一度電子の位置を測定すると予測位置より±100mのどこかで1/2000mm程度の誤差で位置が確定しますが、時間が経過するとまた電子の位置は不確定となります。
このように電子の位置を正確に予測することは不可能です。
● これが日常生活のスケールではどの程度になるでしょうか。
野球のボール(質量約150g)で考えます。同じく緑色の光子を1個当てた場合、ボールの速度の不確定さは
\(\Delta v_{x}=\dfrac{1.05\times 10^{-28}}{150\times 10^{-3}}\sim 7.0\times 10^{-34} m/s\)
です。
ボールが晴天の太陽光を真横から受けるとして1秒間で約1.6×1018 個の光子となります。
(太陽光の照度105lx(ルクス)として、1 lx=1.46mWm-2=1.46×10-3Js-1m-2、ボールの断面積 S=πr2=3.14×(3.7cm)2=0.0043m2、光子のエネルギー E=2.48eV=4.0×10-19J)
これだけの光子が同じ方向から一度に衝突したとしても
\(\Delta v_{x}\geq 1.12\times 10^{-15}m/s (=1.12\times 10^{-12}mm/s)\)
となり1秒後の予測位置からのずれは1兆分の1mmで、無視することができます。
不確定性原理は原子や素粒子の微視的世界で考慮する必要があり、身の周りの物体の運動を扱う場合はニュートン力学で十分です。

