時間と空間の幾何学

時間と空間の幾何学　－ミンコフスキー空間－
　ローレンツ変換は時間と空間が混じった変換であるため、3次元の空間に時間座標を加えた4次元空間を考えていきます。ミンコフスキーが導入したもので、ミンコフスキーの時空世界とも言われています。

ローレンツ変換を以下のように取ります。

y’=y、z’=z ですので　(x, ct)、(x’, ct’)の関係を以下の手順で図示していきます。

［Ⅰ］ S系で横軸を x、縦軸を ct にとります。

［Ⅱ］ S系に S’系の x’ 軸を記入します。
　　　　x’ 軸は ct’＝0となる直線ですので、④ 式より ct=βx となりS系では傾き
　　　 β (<1) の 直線となります。
　
［Ⅲ］ S系に S’系のct’ 軸を記入します。 ct’ 軸は x’＝0となる直線ですので、
　　　① 式より \(ct=\dfrac{1}{\beta }x\) となりS系では傾き \(\dfrac{1}{\beta }\) (>1)の直線となります。

［Ⅳ］ 目盛：
　　　S’ 系でx’ 軸上のx’ ＝1、ct’ 軸上のct’＝1の目盛の位置を求めます。
　　　x’ ＝1 の目盛は ct’＝0 の直線上にあるので、①’ 、④’ 式に x’ ＝1、ct’＝0
　　を代入すると
　　　S系の座標　\(x=\dfrac{1}{\sqrt{1-\beta ^{2}}}\)、\(ct=\dfrac{\beta }{\sqrt{1-\beta ^{2}}}\)　が得られます。
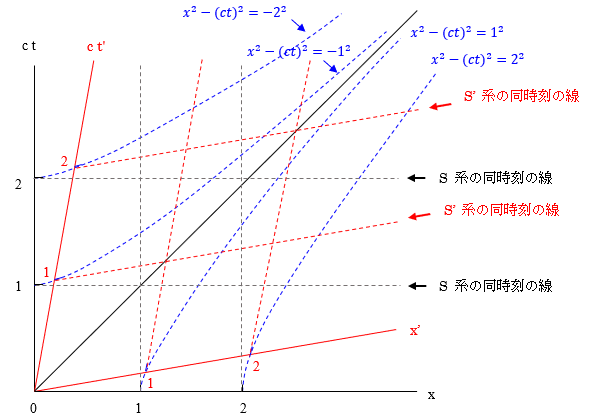
　　　\(x^{2}-\left( ct\right) ^{2}=1^{2}\)　ですので　x’ 軸と双曲線　\(x^{2}-\left( ct\right) ^{2}=1^{2}\)
　　が交わる点が x’ ＝1 となります。

　　　cx’ ＝1 の目盛は x’＝0 の直線上にあるので、①’ 、④’ 式に x’ ＝0、ct’＝1
　　を代入すると
　　S系の座標　\(x=\dfrac{\beta}{\sqrt{1-\beta ^{2}}}\)、\(ct=\dfrac{1}{\sqrt{1-\beta ^{2}}}\)　　が得られます。
　　　\(x^{2}-\left( ct\right) ^{2}=-1^{2}\)　ですので　ct’ 軸と双曲線　\(x^{2}-\left( ct\right) ^{2}=-1^{2}\)
　　が交わる点が ct’ ＝1となります。

以下同様にS系で S’ 系の x’＝2、ct’ ＝2 等の目盛の位置を決めることができます。

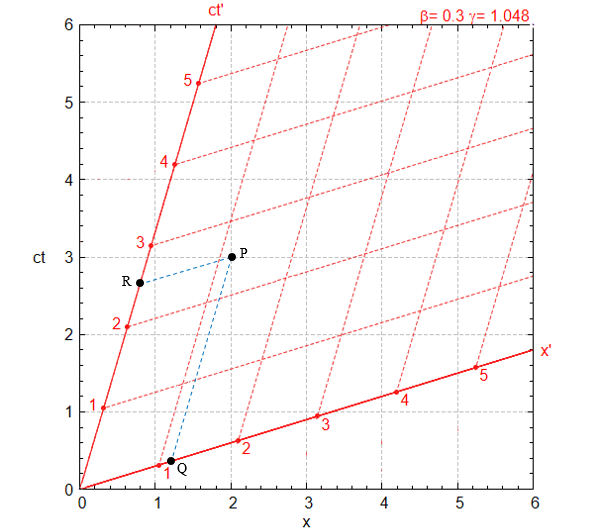
　例としてβ＝0.3、S系で x＝2、ct＝3 で起こった事象は点Pで表されます。

　　これをS’系で見ると、位置は点Q、時刻は点Rとなります。
　　 Q の値は x’＝1.2、Rの値はct’＝2.5 ぐらいでしょうか。

　　正確には x＝2、ct＝3、β＝0.3 をそれぞれ ①、④ に代入して

　　\(x’=\dfrac{2-0.3\times 3}{\sqrt{1-0.3^{2}}}=1.153\)　　　\(ct’=\dfrac{3-0.3\times 2}{\sqrt{1-0.3^{2}}}=2.516\)

　　となり、図で読取った値と一致します。

ミンコフスキー空間で見た
「運動する系の時間の遅れ、空間の短縮」

　図は β＝0.3 を使用しますが、一般的に成り立つ関係です。

運動する系の時間の遅れ

　[A]　S系を基準として時刻がT_Aのとき、S’系の原点の時刻T_A’
　　（S’系が運動している場合です。）
　　下図の例で比較すれば T_A～5.45、T_A’～5.2 くらいですので T_A’＜T_A であるのが分かります。

　　ローレンツ変換の式 ④’ に x’＝0 を代入して

　　\(cT_{A}=\dfrac{cT_{A}’}{\sqrt{1-\beta ^{2}}}\)　より　\(T_{A}’=T_{A}\sqrt{1-\beta ^{2}}\)

　　 T_A’＜T_A　となり S’系の時間が遅れます。

　[B]　S’系を基準として時刻が T_B’ のとき、S系の原点の時刻 T_B
　　（S系が運動している場合です。）
　　下図の例で比較すれば T_B’～4.5、T_B～4.3 くらいですのでT_B＜T_B’ であるのが分かります。

　　ローレンツ変換の式 ④ に x＝0 を代入して

　　\(cT_{B}’=\dfrac{cT_{B}}{\sqrt{1-\beta ^{2}}}\)　より　\(T_{B}=T_{B}’\sqrt{1-\beta ^{2}}\)

　　 T_B＜T_B’　となり S’系の時間が遅れます。

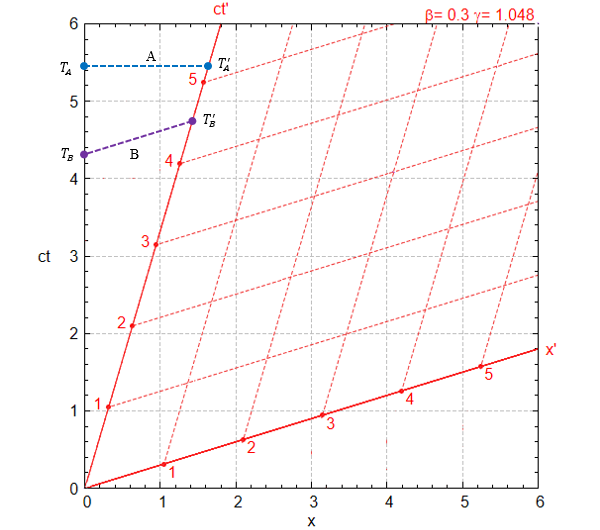
　S系を基準にとるとS’系の時間が遅れ、S’系を基準にとるとS系の時間が遅れます。

運動する空間の短縮

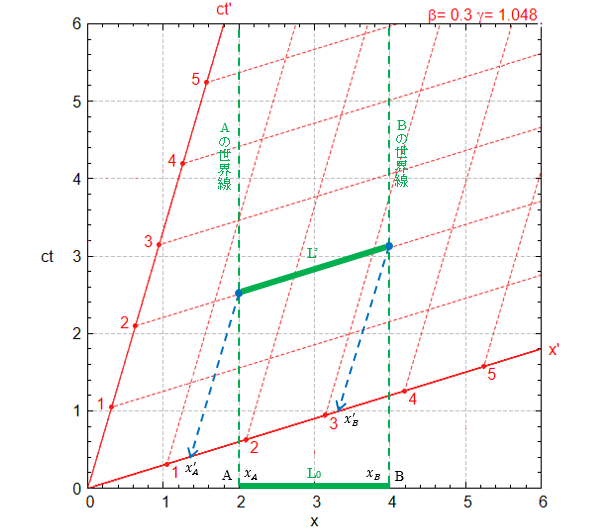
　S系に静止している長さ L₀ の棒を S’系で見ます。

　棒の一端Aの位置をx_A（＝一定）、他端Bの位置をx_B（＝一定）とおくと、時刻ctでの両端の位置は図の直線A、Bで表されます。

　S’系から見ると棒は後方に運動していることになります。

　下図では棒の一端の位置が x_A＝2、他端の位置が x_B＝4になっていますので L₀＝2です。

　S’系で棒の長さを測定する場合は、両端の座標を「同時に」読み取り、その差が S’系で観測したの棒の長さとなります。棒は S’系で後方に運動しているので座標の読み取りで両端の時間差が生じると正確な測定値は得られません。S’系で「同時に」読み取ることが重要です。

　時刻はいつでもよいので、図のようにS’系でct’＝2の時刻でABの座標を読み取ります。　図で正確に読み取ることは難しいのですが、x_A‘ ≒1.3 、x_B‘≒3.2  くらいでしょうか。
　S’系で測定した棒の長さ L’ は L’＝ x_B’－x_A’＝3.2－1.3=1.9＜2となり S’系で見ると短縮しています。図では見かけ上 L’ の方が長く見えますが、x軸とx’軸の目盛幅が違っていますので値としてはL’ の方が小さくなります。
　短縮の割合は　L’/L₀～1.9/2＝0.95 となりますが、読み取り精度があまりよくないので誤差は大きいです。

　　ローレンツ変換の式 ①’ より時刻を ct’ とすれば

　　\(x_{B}-x_{A}=\dfrac{x_{B}’+\beta \left( ct’\right) }{\sqrt{1-\beta ^{2}}}-\dfrac{x_{A}’+\beta \left( ct’\right) }{\sqrt{1-\beta ^{2}}}=\dfrac{x_{B}’-x_{A}’}{\sqrt{1-\beta ^{2}}}\)

　　\(x_{B}-x_{A}=L_{0}\)、\(x_{B}’-x_{A}’=L’\)　から

　　\(L’=L_{0}\sqrt{1-\beta ^{2}}\)、\(L'<L_{0}\)　が得られます。

S’系に静止している長さ L₀ の棒を S系で見ます。

　棒の一端 A’ の位置を x_A‘（＝一定）、他端 B’の位置を x_B‘（＝一定）とおくと、時刻 ct’での両端の位置は図の直線 A’、B’で表されます。

　S系から見ると棒は後方に運動していることになります。

下図では棒の一端の位置が x_A‘＝1、他端の位置が x_B‘＝3 になっていますので L₀＝2です。

　S系で棒の長さを測定する場合は、両端の座標を「同時に」読み取り、その差が S系で観測したの棒の長さとなります。棒は S系で後方に運動しているので座標の読み取りで両端の時間差が生じると正確な測定値は得られません。S系で「同時に」読み取ることが重要です。

　S系で ct＝3 の時刻でA’、B’の座標を読み取ります。　図で正確に読み取ることは難しいのですが、x_A は 1.8 より少し大きめ 、x_B は 3.8 より少し小さいくらいなので、 x_B－x_A＜2 であることは確かです。

　　ローレンツ変換の式 ①’より時刻を ct とすれば

　　\(x_{B}’-x_{A}’=\dfrac{x_{B}-\beta \left( ct\right) }{\sqrt{1-\beta ^{2}}}-\dfrac{x_{A}-\beta \left( ct\right) }{\sqrt{1-\beta ^{2}}}=\dfrac{x_{B}-x_{A}}{\sqrt{1-\beta ^{2}}}\)

　　\(x_{B}’-x_{A}’=L_{0}\)、\(x_{B}-x_{A}=L’\)　から

　　\(L’=L_{0}\sqrt{1-\beta ^{2}}\)、\(L'<L_{0}\)　が得られます。

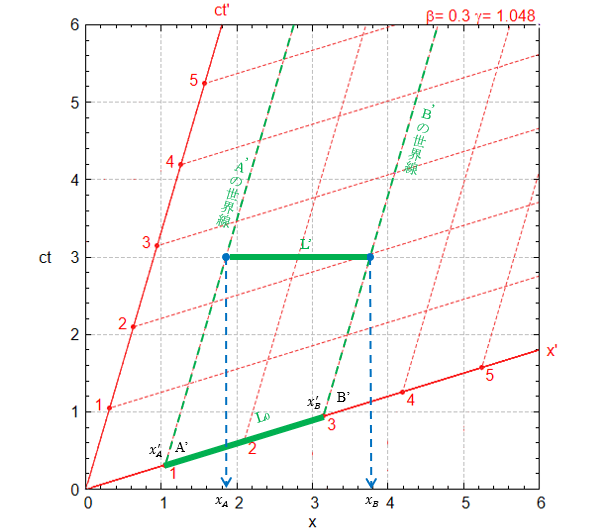
　S系を基準にとると S’系の空間が短縮し、S’系を基準にとると S系の空間が短縮します。

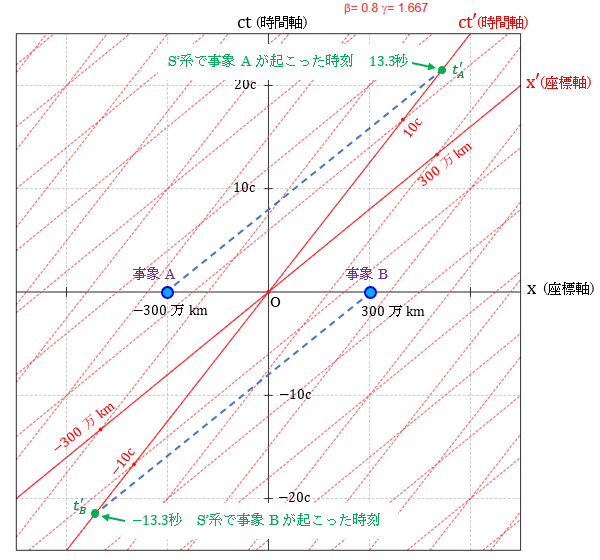
ミンコフスキー空間で見た「同時刻の相対性」

　　同時刻の定義で示した例をミンコフスキー空間で見ていきます。
　β＝0.8ですので、ローレンツ変換の軸の傾きが大きくなり図ではちょっと見づらくなります。

　S系で点Aの位置を x＝－300万km、点Bの位置をx＝300万kmとします。
　S系を基準として ct＝0のとき ABで同時に起こった事象は下図の事象A、事象Bの点で表されます。

　S’系を基準としたとき、それぞれの事象が起こった時刻は t_A’、t_B’ で下図緑色の点です。

　図で事象Bが先に起こり、時刻はt_B’≒－13秒（Oに到達する約13秒前）、その後で事象Aが時刻t_A’＝13秒（Oを通過後13秒後）に起こることが読み取れます。