相対性理論 時間と空間の幾何学
時間と空間の幾何学 －ミンコフスキー空間－ ローレンツ変換は時間と空間が混じった変換であるため、3次元の空間に時間座標を加えた4次元空間を考えていきます。ミンコフスキーが導入したもので、ミンコフスキーの時空世界とも言われています。 ローレン...
相対性理論
相対性理論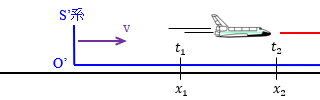 
相対性理論 ローレンツ変換で導かれる事
ローレンツ変換から導かれるいくつかの事柄を求めていきます。ここでは \(\dfrac{v}{c}=\beta\) とおいたローレンツ変換の式を用います。● 時間の遅れ：運動する系は時間が遅れる S系を基準として、S系の時刻が t のときS’...
相対性理論 ローレンツ変換
ローレンツ変換の式を求めます。 \(x'=\dfrac{x-vt}{\sqrt{1-\dfrac{v^{2}}{c^{2}}}}\) \(t'=\dfrac{t-\dfrac{v}{c^{2}}x}{\sqrt{1-\dfrac{v...
相対性理論 同時刻の定義と相対性
同時刻の定義 2つの異なる地点A,Bで時計の時刻を正確に合わせるときはどのようにすれば良いでしょうか。AB間の距離が一定のとき Bの時計をAに合わせます。 ① AB間の距離が分かっている場合（Lとおきます） Aの時計で時刻12時のとき、光で...
相対性理論 時間のパラドックス
相対性理論によれば、運動する系には時間の遅れが生じます。系の速さを v、光速をcとおけば、運動する系の時間の遅れは \(t'=\sqrt{1-\left( \dfrac{v}{c}\right) ^{2}}t\) （t は v=0 での...