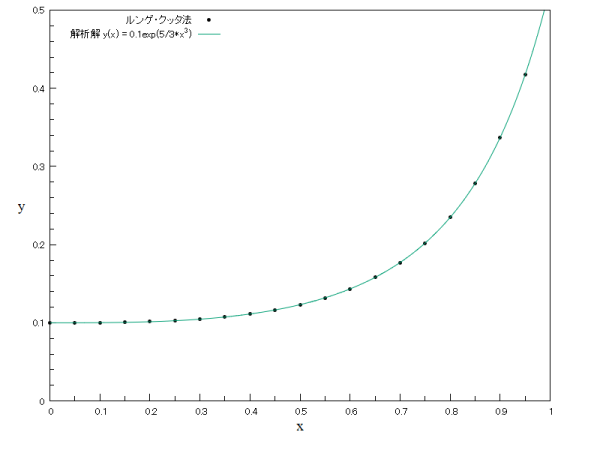
常微分方程式の数値解を求める手法のひとつです。
オイラー法が1次の精度であるのに対して、ルンゲ・クッタ法では4次の精度まで得られます。
y が x の未知関数 \( y=y\left( x\right) \) で、\( \dfrac{dy}{dx}=f\left( x,y\right) \) が与えられているとき、
\(x=x_{i} \) で \( y=y\left( x_{i}\right) \) のとき、\( x_{i+1}=x_{i}+h \) での y の値 \( y\left( x_{i+1}\right) \) を次の式で近似したものです。
\(k_{1}=hf\left( x_{i},y_{i}\right)\)
\(k_{2}=hf\left( x_{i}+\dfrac{h}{2},y_{i}+\dfrac{k_{1}}{2}\right)\)
\(k_{3}=hf\left( x_{i}+\dfrac{h}{2},y_{i}+\dfrac{k_{2}}{2}\right)\)
\(k_{4}=hf\left( x_{i}+h,y_{i}+k_{3}\right)\)
\(x_{i+1}=x_{i}+h\)
\(y_{i+1}=y_{i}+\dfrac{1}{6} \left( k_{1}+2k_{2}+2k_{3}+k_{4}\right)\)
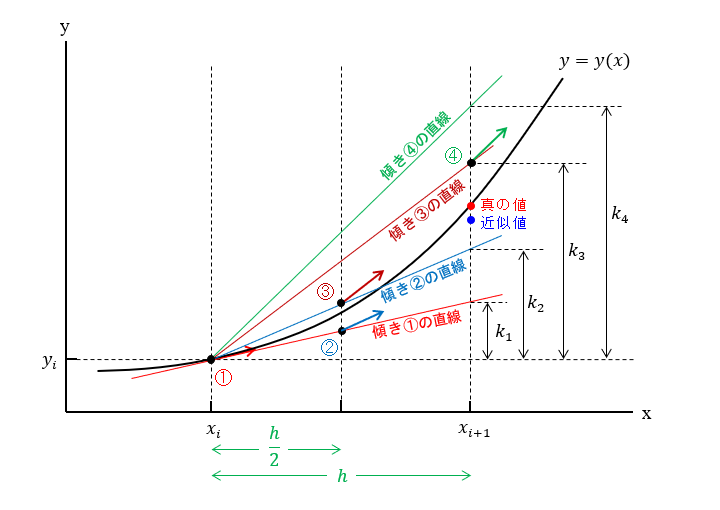
\(k_{1}, k_{2}, k_{3}, k_{4}\) を図で表すと下のようになります。
\(x_{i}\leq x\leq x_{i+1}\) で ①~④ の4点で傾きを求め、点① \(\left( x_{i},y_{i}\right)\) からそれぞれの傾きを使って \(x_{i+1}( =x_{i}+h)\) での y の変化量を求めていきます。
点① \(\left( x_{i},y_{i}\right)\) で傾きを求めます(赤い矢印)。
点① からこの傾きを使って求めた \(x_{i+1}\) での y の変化量が \(k_{1}\) です。
点② \(\left( x_{i}+\dfrac{h}{2},y_{i}+\dfrac{k_{1}}{2}\right)\) で傾きを求めます(青い矢印)。
点①からこの傾きを使って求めた \(x_{i+1}\) での y の変化量が \(k_{2}\) です。
点③ \(\left( x_{i}+\dfrac{h}{2},y_{i}+\dfrac{k_{2}}{2}\right)\) で傾きを求めます(えんじ色の矢印)。
点①からこの傾きを使って求めた \(x_{i+1}\) での y の変化量が \(k_{3}\) です。
点④ \(\left( x_{i}+h,y_{i}+k_{3}\right)\) で傾きを求めます(緑色の矢印)。
点① からこの傾きを使って求めた \(x_{i+1}\) での y の変化量が \(k_{4}\) です。
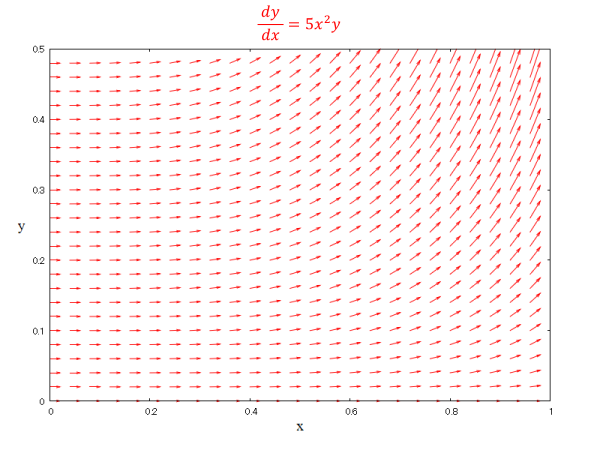
例として微分方程式 \(\dfrac{dy}{dx}=5x^{2}y\) の解をルンゲ・クッタ法で求めていきます。
ここで \(f\left( x,y\right) =5x^{2}y\) は点 \(( x, y)\) での \( y\left( x\right) \) の傾きで、主な点での傾きを図で 表すと下のようになります。矢印が傾きで、これらが接線になるように結んだ曲線がこの微分方程式の解です。解は無数にあります。
この微分方程式の一般解は \(y=A\exp \left( \dfrac{5}{3}x^{3}\right)\) です。
\(x=0\) のとき、それぞれ \(y=0.1, 0.2, 0.3\) を通る3つの特殊解
\(y=0.1 \exp \left( \dfrac{5}{3}x^{3}\right), y=0.2 \exp \left( \dfrac{5}{3}x^{3}\right), y=0.3 \exp \left( \dfrac{5}{3}x^{3}\right)\)
を図に書き込むと以下のようになります。いずれも接線が矢印方向となっています。
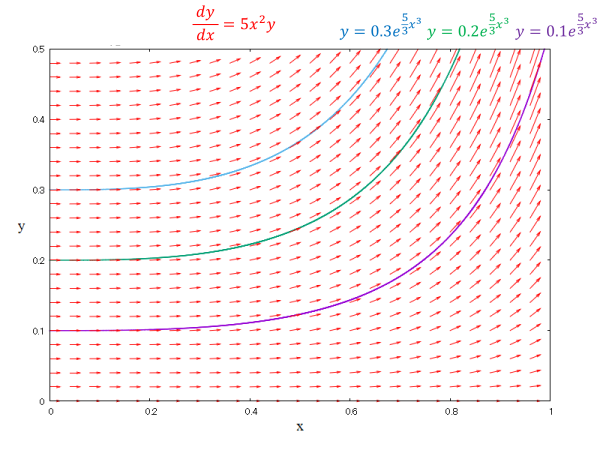
ここで、\(x=0\) のとき、\(y=0.1\) を通る解をルンゲ・クッタ法で求めます。
プログラムのソース(C++)です。\(h=0.05\) としています。
#include <stdio.h>
#include <math.h>
//--- dy/dx=5*x*x*y, y=C*exp(5/3*x*x*x)
// 特別解 x=0.0,y=0.1 y=0.1*exp(5/3*x*x*x)
double f(double x,double y);
double y_true(double x);
int main(){
int i,N;
double x,y,h;
double dy;
double k1,k2,k3,k4;
h = 0.05; //刻み幅
N = (1.0-0.0)/h;
printf(" x y_RK y_true dy\n");
//--- 初期値 ---
x = 0.0;
y = 0.1;
dy = y-y_true(x);
printf("%7.5lf %10.7lf %10.7lf %10.7lf\n",x,y,y_true(x),dy);
//--------------
for (i=0; i<N; i++){
k1 = h*f(x,y);
k2 = h*f(x+h/2.0,y+k1/2.0);
k3 = h*f(x+h/2.0,y+k2/2.0);
k4 = h*f(x+h,y+k3);
x = x+h;
y = y+(k1+2.0*k2+2.0*k3+k4)/6.0;
dy = y-y_true(x); // 解析解との差
printf("%7.5lf %10.7lf %10.7lf %10.7lf\n",x,y,y_true(x),dy);
}
}
double f(double x,double y){
return 5.0*x*x*y;
}
//--- 解析解 ---
double y_true(double x){
return 0.1*exp(5.0/3.0*x*x*x);
}結果です。比較的簡単な式ですので実際の値とよく一致しています。
x y_RK y_true dy
0.00000 0.1000000 0.1000000 0.0000000
0.05000 0.1000208 0.1000208 -0.0000000
0.10000 0.1001668 0.1001668 -0.0000000
0.15000 0.1005641 0.1005641 -0.0000000
0.20000 0.1013423 0.1013423 -0.0000000
0.25000 0.1026384 0.1026384 -0.0000000
0.30000 0.1046028 0.1046028 -0.0000000
0.35000 0.1074073 0.1074073 -0.0000000
0.40000 0.1112563 0.1112563 -0.0000000
0.45000 0.1164015 0.1164015 -0.0000000
0.50000 0.1231624 0.1231624 -0.0000000
0.55000 0.1319551 0.1319551 -0.0000000
0.60000 0.1433329 0.1433329 -0.0000000
0.65000 0.1580448 0.1580448 -0.0000000
0.70000 0.1771216 0.1771217 -0.0000001
0.75000 0.2020054 0.2020056 -0.0000001
0.80000 0.2347456 0.2347459 -0.0000003
0.85000 0.2783027 0.2783034 -0.0000007
0.90000 0.3370279 0.3370294 -0.0000015
0.95000 0.4174317 0.4174349 -0.0000032
1.00000 0.5294421 0.5294490 -0.0000069図で表すと下のようになります。